(Created: March 12th, 2019)
BehindMyEyes365@gmail.com
Welcome to my webpage!
----
Check out my new javaScript games under the 'e' and the 'm' headers.
For full keyboards only. WASD + QE + RF and up/down/left/right controls for both games.
The letter 'X' resets to the original position.
Touch screen controls coming soon...
----
I have posted here several pictures I've created with my fractal-generating program, a few pieces of my writing, different excerpts from books I have read, and several quotations from various people I admire. Because it was wanting to share with you the pictures I've created, that made me first form this site, I'd like to start with that...
Years ago I first stumbled upon Beniot Mandelbrot's fractal, and I was struck by its intricate beauty. The initial impression it left on me spurred me to want to learn more about what it represented, and how it was rendered. It turns out that Mandelbrot's initial creation was just the tip of an ice berg so enormous, that I've been absorbed with it ever since.

The broken-flow of it's undulating boundry captures the attention in a marvalous way. Mandelbrot himself was interested in "the art of roughness" and the "uncontrolled element in life" (*Wikipedia) and it is plain to see how very-much present these themes are, in this eponymous fractal. We have IBM to thank for providing Mandelbrot with the computer-power necessary to calculate this complex mathmatical set, for as my Uncle said, "there aren't enough monks" available to hack out something like this by hand.
The Mandelbrot set is created by the recursive iteration of the function Z = Z^2 + C where "Z" and "C" are complex numbers. By taking the output of one iteration and using it as the input of the next, one forms a succesive list of numbers that may or may not increase to infinity. The intial paramters used to start the process are sorted into two groups based on this behavior, and the numbers that generate outputs that remain bounded are included in the set. All others are outside this group. In the picture shown, the white color represets all initial numbers, that when iterated endlessly, remain bounded, and the black color represets the numbers that do not.

Of course, the colors we ascribe to the "in-group" and the "out-group" are arbitrary. We can in fact make them anything we want. The weird and wonderful thing is, though, the equation itself that we use to generate the Mandelbrot set is tweekable, and by varying the elements contained within the expression we can get a wide variety of pictures using the same basic principle.
The second picture shown is an example of what happens when you take the original equation, Z = Z^2 + C, and change it slightly to Z = Z^5 + C. I also switched the color paramters to reflect the speed at which certain clusters of numbers swell passed the boundry I assigned. The black outline jumped passed the threshold with the smallest number of "recursions," if you will. The white color ballooned at the second quickest rate. The green just barely failed to remain bounded, and the red color remained bounded regardless of how many iterations I calculated. What I wanted to show with this is the drastic change in the composition of the image that resulted from such a small change in the original function. Imagine wildly convoluted expressions that included trig functions, or natual logarithms, or square roots. The posiibilities of different combonations are in fact endless!

I hope you get at least a touch of the "awesome" that I feel when I look at pictures like these. The fact that they are the result of the application of Mathematics and Computer technology makes them, for me at least, even better then if they were meticulously crafted by the Human hand. The idea of "Recreational Mathematics" makes me laugh all most. At how absurd that seems to my dull-witted ears, but also, how miraculous it is at the same time that a concept like that even exists in the first place. Math for pleasure and recreation! Who would of thought... All it takes is a little work upfront to create the Html/javaScript framework that does the hard work of calculation, and away you go.

Here's one more, that I'll explain further in the section on Fractals deeper in my website. It applies the rediculous function Z = (Ln(Ln(Ln(Ln( {(5 + 10i)+(Z^4)} / Cot(Z^3) )))). A form that is quite striking, if I do say. Both the equation itself and the resulting picture. Using the rgba(0,0,0,1) spectrum, the color is rendered using a method that equates the saturation of color to the rate at which the function increases towards infinity. For those of you that are familiar with javaScript: "rgba("+complexMod+",0,0,1)" Where "complexMod" is a variable that contains the modulus of the complex number that is the result of each iteration.
Like I mentioned at the beginning, the beauty of these fractals, and the javaScript program I wrote to create them are the main reason I made this website. But as more time passed I decided to include some writing I've done and a few quotes I've gathered from people like Carl Jung, Ralph Waldo Emerson, and Ken Wilbur to name a few. Also, I've included excerpts from the writings of Stanislav Grof, William James and others, and as you puruse my site I hope you find enjoyment, as I have, in these wonderful things. If you have any feedback on my content, whether from my own mind, or borrowed from others, please email me and let me know.
Creating a fractal
In order to render one of these marvelous pictures you need to know a little bit more about the recursive nature of the functions used to create them. As I mentioned above, when we plug a number into our function and make a calculation, the resulting answer, the "output," is reused as the "input" for the next calculation. This is what it means to be recursive, and each time you recompute the function using the new input, it is call an "iteration." I'll give you an example to better illustrate what I mean.
Let us use Z = Z^2 + C as our complex function, and the complex number (0.23 + 0.55i) as the initial value of C. The number here, that you begin with, is called the "seed." The Z value of the Z^2 term will start at (0 + 0i).
Z = (0 + 0i)^2 + (0.23 + 0.55i)
ans: Z = 0.23 + 0.55i
The new Z value: 0.23 + 0.55i is now placed within the Z^2 term for the next iteration, while C remains the same.
Z = (0.23 + 0.55i)^2 + (0.23 + 0.55i)
ans: Z = -0.0196 + 0.803i
Again, the new value is placed into the Z^2 term, while C remains the same.
Z = (-0.0196 + 0.803i)^2 + (0.23 + 0.55i)
ans: Z = -0.414 + 0.519i
And again...
Z = (-0.414 + 0.519i)^2 + (0.23 + 0.55i)
ans: Z = 0.132 + 0.120i
And so on and so forth for as many times as you'd like. When actually creating a fractal though, the practical limitations of computing power will constrain the number of iterations you calculate when generating a picture. I use the "Canvas" element within the HTML to create my graphics, and each pixel gets rendered independently. So, imagine a Canvas-patch 800 pixels by 800 pixels large, thats 64000 individual pixels that have to be worked through. If each were to recieve 5 iterations of your function, that would amount to 320,000 total iterations. Not a small number. Now, mind you, when creating a fractal, there is more to the program then just the tabulation of numbers, as I will soon show you. Other parts of the program will have to be processed along with the simple number-crunching for every iteration, so the work can really pile up.

Another aspect of fractal design I mentioned above was the idea of bounded and unbounded progressions; Whether or not the magnitude of your result remains below the threshold you assign, or increases beyond it. This is done by applying the Pythagorean theorom, using the two numerical values within your complex result, to figure what is called the "modulus" of that number.
modulus = sqrt(real*real + imaginary*imaginary)
This number is computed for each answer you get, for every iteration you compute, and is checked against the boundry number each time. When computing the Mandelbrot set, the maximum modulus allowed, for any complex number within the set, is usually 2. Enough people have played around with it's function (Z = Z^2 + C) to know that any number that does, in fact, breach this particular magnitude, will keep growing for as long as you keep replugging in the numbers. People have found this to be true, and others have verified. An interesting point though, the numbers that actually fall in the set, and remain below the limit of 2, will always and forever remain bounded no matter how many times you reiterate a particular number that is a member of the set. Curious indeed!
When you decide to create random functions of your own though, this fact, whether or not repeated iterations remain bounded over the long run, isn't known to you. So, the magic number is set arbitrarily. Let me give you an example of computing the modulus of a complex number. We'll use the values from the progression above.
Z1 = 0.23 + 0.55i
mod = sqrt(0.23*0.23 + 0.55*0.55)
mod = 0.596
Z2 = -0.0196 + 0.803i
mod = sqrt(-0.0196*-0.0196 + 0.803*0.803)
mod = 0.803
Z3 = -0.414 + 0.519i
mod = sqrt(-0.414*-0.414 + 0.519*0.519)
mod = 0.664
Z4 = 0.132 + 0.120i
mod = sqrt(0.132*0.132 + 0.120*0.120)
mod = 0.178
You can see how the modulus bounces around a bit, but it will always be a positive, real number. This is due to the Pythagorean theorom itself, which you can see involves the squares of the two individual components before the root is taken.
When computing a fractal, it is the value of this modulus that ultimately determines the color of each pixel within the viewing frame. If, lets say, after 10 iterations, the modulus of the number never reaches above 2 we assign to that pixel the color of white, and if it does, at any time during those 10 computations, reach above that number, the sequence is stopped, the color assigned is black, and the program moves onto the next number/pixel. As I've mentioned before, the colors you choose as the programer are up to you.

A brief introduction to the calculation of recursive, complex iterations, and the finding of the modulus and what not, was important to give you a sense of where we are coming from. For, when we try to set up a javaScript program to render our creations, we'll need to know, on a basic level, this specific operation. It sits at the heart of our process. For the purposes of this conversation I've already assumed that the reader knows what a complex number actually is, and going forward I'll have to assume as well, a basic understanding of HTML, and also of the javaScript programing language. The examples I show of actual code will be displayed in an image format, either *.jpeg, or *.png, in order to please the various browsers and their security concerns.
Programming in javaScript
The next section will discuss the basic code necessary to program a simple fractal generator. As I said, I'm going to post simple image files that capture the part of the code I'm talking about. The complex numbers are handled using code based on an example given by Jan Hartigan, in the article "Creating a JavaScript ComplexNumber Class," fround on this site. I first created my program back in early 2019, and as of then the page was still active. Either way, I'll have the salient information anyhow.

This image shows the basic html skeleton, along with the the script example I got from the website I referenced. Since the initial inception of my fractal program I've added other functions to this rather sparse set, using this example as a template. Over time I've written trig functions, square root functions, and the natural log function, and added these to increase the dynamic range of the resulting fractals.
If you were to rewrite this into your own html document, and load the page, you would have printed in your devTool console (f12) three different figures. The first being the summation of the two complex numbers listed as "complex1" and "complex2", the second being the product of them, and the third number would be the modulus of the first complex number (complex1).
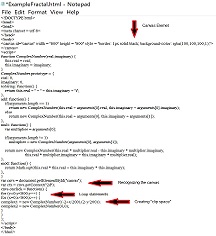
After coding the javaScript that's necessary to work on the complex plane, the next step is to insert the canvas element onto your page, and create what is called a "clip space" to convert the raw canvas into a Cartesian coordinate system with its origin in the middle of the page, instead of starting in the upper left hand corner. Within this new space, the (x,y) coordinate of each pixel is used to create a complex number, which is then used in the equation we iterate to create the image.
Notice how the ComplexNumber function is called for each x and y count, and how a little algebraic magic is used to transform each value into a new number within our clip space. The first pixel on our canvas, with a coordinate of (0,0) in "canvas-space", has now been transformed into the coordinate (-2,0), within our clip space. The canvas coordinate (400,400) would be (0,0) in clip space, and (800,800) would become (2,-2). The denominator here is calculated by taking either the width or height dimension of the canvas (in this case the canvas is square so both dimensions are 800 pixels accross) and dividing that by the corresponding width or height of the newly created clip space. In our case a total range of -2 through +2 amounts to 4 total units; 800 / 4 = 200.

Next, we must input each new complex number into our recursive function, and add a third loop statement to cycle through multiple iterations of this function. As I stated above, the Mandelbrot fractal is generated using the equation Z = Z^2 + C. So this is what we will use. After each modulus is determined, it is compared with two different conditions to see if it matches, and if it does, what action to perform. In this case, the first condition doesn't actually reference the modulus, but asks whether or not the "j-loop" counter has reached or exceeded its 50th and final iteration. If it meets this condition, before the modulus ever rises above 2, it colors that particular pixel white (rgba(255,255,255,1), stops the j-loop, and returns to the next x or y count.
If, before 50 iterations are calculated, the modulus of the result ever exceeds 2, the j-loop is stopped, the pixel is colored black (rgba(0,0,0,1), and the program cycles back to the next x or y count. You can see here that the color of each pixel is arbitrary, and so is the value of the threshold that the modulus may or may not cross. If you click here, I've included a page with the javaScript up and running so you can take a look at the code of a full and complete fractal-generator. Of course, javaScript must be enabled on your device. The code I use is a bit old, and I guess, kind of sloppy. Variables aren't really indicated specifically with the "var" heading, and I know some of the other code is outdated compared with newer versions. But it works. It's a very simple set up, and it should work on just about every machine, I think. I've included an extra paragraph tag in the code to announce when the program is finished running. You need to click on the canvas itself to activate it all.